HKCERT CTF 2022 – Base64 Encryption

The challenge looks deceptively simple. Chinese has over 50,000 characters. Base64 just has 64. So it should be easy right?

Haha nope. It's not as trivial as I thought.

Description

200 points. 3/5 ⭐️. 6/311 solves.

People said that base64 is an encoding, not an encryption. Did they have a misconception about that?

If you believe that base64 is just an encoding, then convince me that you are able to "decode" the article (which is in English).

Regardless, the challenge author is kind enough to provide a clue in the description: the plaintext is an article in English. We’ll see how this helps us later on.

Analysis

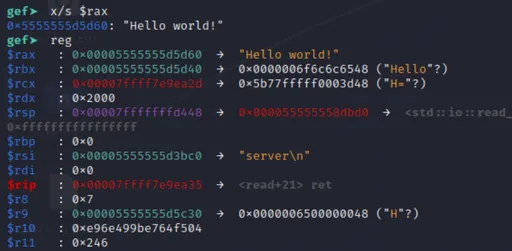
We’re provided with an encryption script chall.py (written in Python), along with the generated ciphertext message.enc.txt.

• The script first encodes the plaintext in English:

  encoded = base64.b64encode(message).decode().rstrip('=')

  Python

  ...then "encrypts" it by mapping each Base64 character to another one:

  encrypted = ''.join([charmap[c] for c in encoded])

  Python

• The script uses random.shuffle without seeding. This means we can’t easily reproduce the character mapping (charmap). We’ll need to try harder.

• Although the script reads the plaintext in binary format (open('message.txt', 'rb')), I’m banking on the clue that the plaintext is an English article—so hopefully there aren’t any weird characters.

So how do we go about cracking this? Brute-force will be undoubtedly inefficient as we have $64! \approx 1.27 \times 10^{89}$ mapping combinations to try. It would take years before we have any progress! Also we’d need to look at results to determine if the English looks right (or automate it by checking a word list)—this would take even more time! Regardless, we need to find some other way.

First Steps: Elimination by ASCII Range

Here’s one idea: since the plaintext is an English article, this means that most (if not all) characters are in the printable ASCII range (32-127). This means that the most significant bit (MSB) of each byte cannot be 1. We can use this to create a blacklist of mappings. For example, originally we have 64 possible mappings for the letter A. After blacklisting, we may be left with, say, 16 possible mappings. This drastically reduces the search space.¹

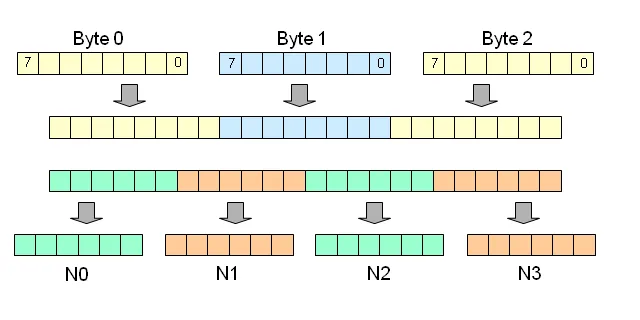
Since Base64 simply maps 8-bits to 6-bits, so 3 characters of ASCII would be translated to 4 characters of Base64.

^{Base64 maps three characters to four. (Source)}

charset = 'ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789+/'

def get_chars_with_mask(m):
    """Get Base64 chars which are masked with m."""
    return {c for i, c in enumerate(charset) if (i & m) == m}

# List the 4 Base64 positions. We'll cycle through these positions (i.e. i % 4).
msbs = [0b100000, 0b001000, 0b000010, 0b000000]

# Get impossible characters for each position.
subchars = [get_chars_with_mask(m) for m in msbs]

# Create a blacklist for each Base64 char.
# e.g. blacklist['A'] returns the set of chars which 'A' can NOT map to.
blacklist = {c: set() for c in charset}

# Loop through each char in the shuffled Base64 text.
for i, c in enumerate(txt):
    # Ignore char mappings which have '1' in corresponding msb.
    # These can't map to a printable ASCII char.
    blacklist[c] |= subchars[i % 4]

# Invert the blacklist to get a dictionary of possible mappings.
# e.g. whitelist['A'] returns the set of chars which 'A' CAN map to.
whitelist = {k: set(charset) - v for k, v in blacklist.items()}

We can check the mappings we’ve eliminated:

print(''.join(sorted(blacklist['J'])))
# '+/0123456789CDGHKLOPSTWXabefghijklmnopqrstuvwxyz'

And that means the letter J can only map to:

print(''.join(sorted(whitelist['J']))
# 'ABEFIJMNQRUVYZcd'

Neat! This will help us later on (when we resort to blatant educated guessing).

We can do a similar thing on the low end. Again, since the smallest printable ASCII character is 32, this means either the second or third MSBs would be set.²

def get_inverted_chars_with_mask(m):
    return {c for i, c in enumerate(charset) if ((2**6 - 1 - i) & m) == m}

# chars that don't have bits set in ascii.
subchars_not_in_ascii = [get_inverted_chars_with_mask(m) for m in in_ascii]

Frequency Analysis with Known Text

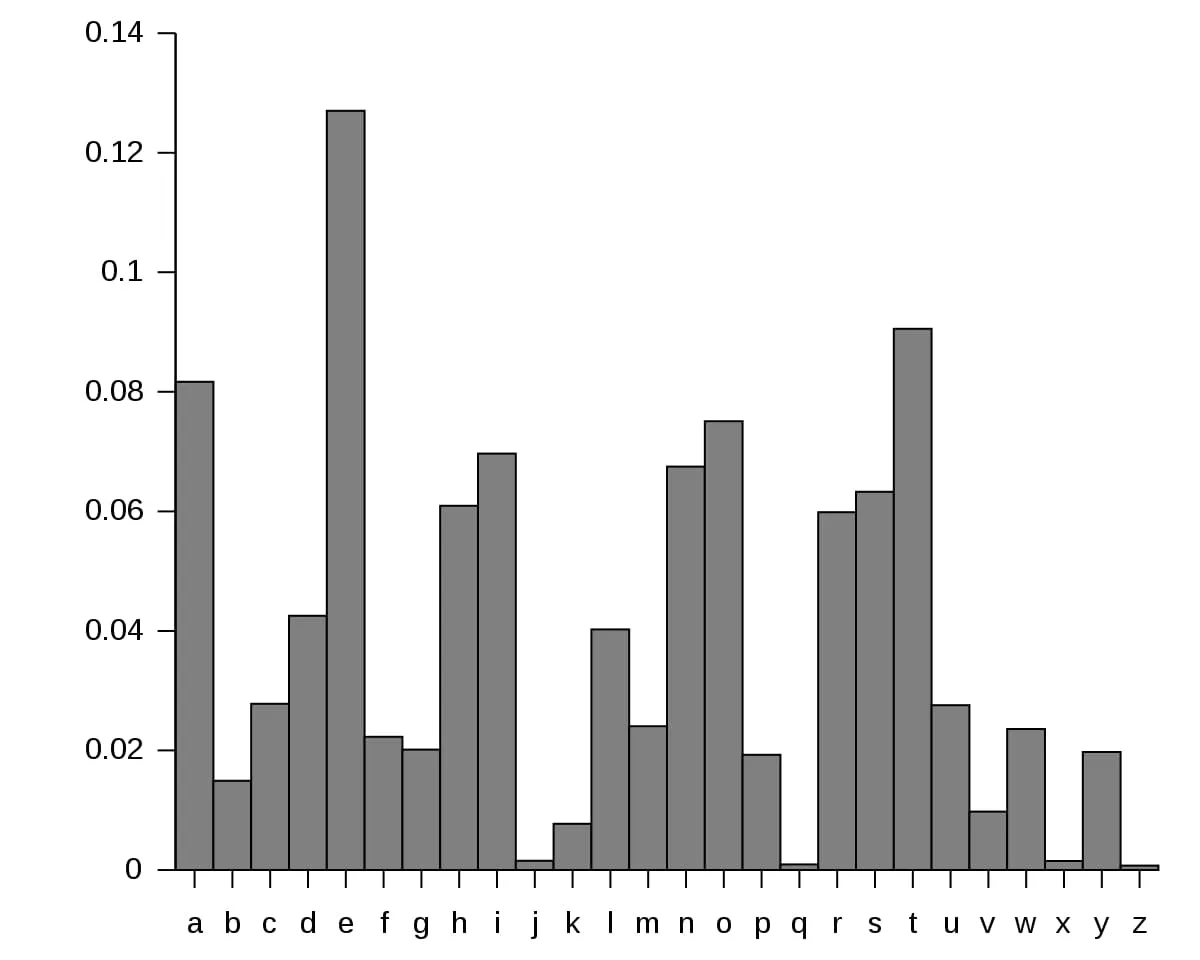
Another idea comes to mind. Remember the plaintext is in English? Well, with English text, some letters appear more frequently than others. The same applies to words and sequences.

^{Frequency of the English alphabet. (Source: Wikipedia.)}

In the same vein, some letters and sequences in the Base64 encoding will also appear more frequently than others.

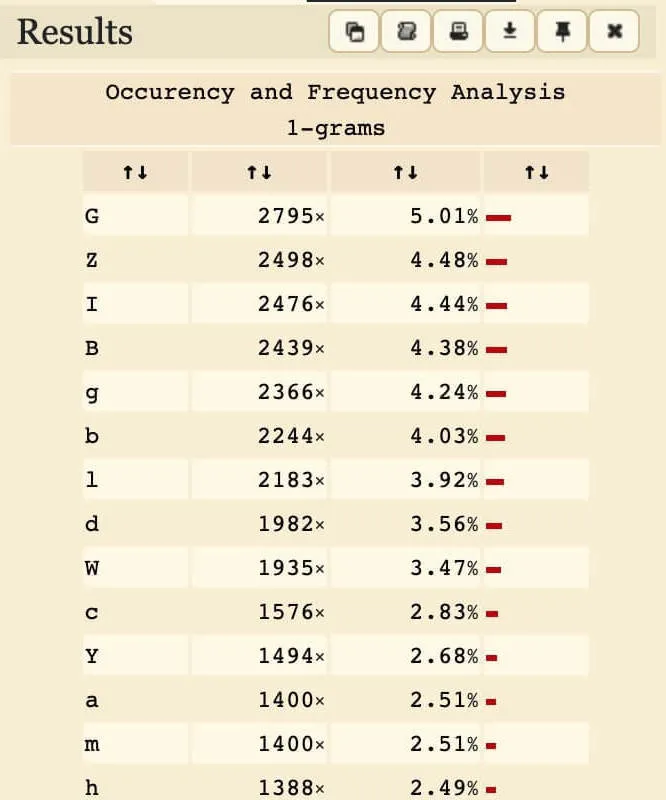
With this in mind, we can compare the ciphertext to the Base64 encoding of some random article (also in English, of course). For this, I copied some articles from CNN Lite (text-only, so it's easier to copy), encoded it, then analysed letter frequencies using dcode.fr. You could use this excellent article as well:

V2UncmUgbm8gc3RyYW5nZXJzIHRvIGxvdmUKWW91IGtub3cgdGhlIHJ1bGVzIGFuZCBzbyBkbyBJIChkbyBJKQpBIGZ1bGwgY29tbWl0bWVudCdzIHdoYXQgSSdtIHRoaW5raW5nIG9mCllvdSB3b3VsZG4ndCBnZXQgdGhpcyBmcm9tIGFueSBvdGhlciBndXkKSSBqdXN0IHdhbm5hIHRlbGwgeW91IGhvdyBJJ20gZmVlbGluZwpHb3R0YSBtYWtlIHlvdSB1bmRlcnN0YW5kCk5ldmVyIGdvbm5hIGdpdmUgeW91IHVwCk5ldmVyIGdvbm5hIGxldCB5b3UgZG93bgpOZXZlciBnb25uYSBydW4gYXJvdW5kIGFuZCBkZXNlcnQgeW91Ck5ldmVyIGdvbm5hIG1ha2UgeW91IGNyeQpOZXZlciBnb25uYSBzYXkgZ29vZGJ5ZQpOZXZlciBnb25uYSB0ZWxsIGEgbGllIGFuZCBodXJ0IHlvdQo=

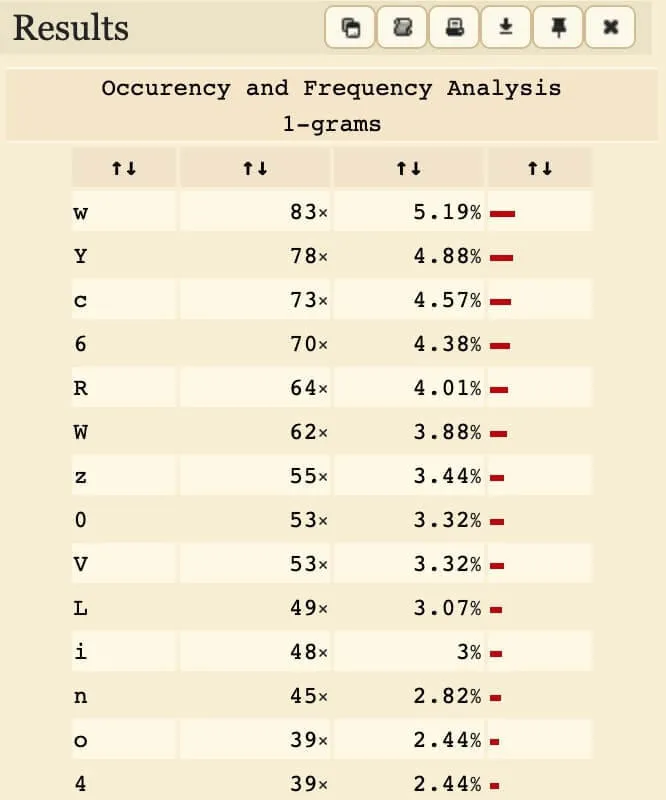
^{Frequency analysis of plain vs. encrypted Base64. Left: CNN Lite articles. Right: Encrypted challenge text.}

From this, we can deduce that 'w' was mapped from 'G' in the original encoding (due to the gap in frequency).

One useful option is the bigrams/n-grams option. We can tell dcode to analyse frequencies of groups of characters with a sliding window. This is useful to identify words and sequences.

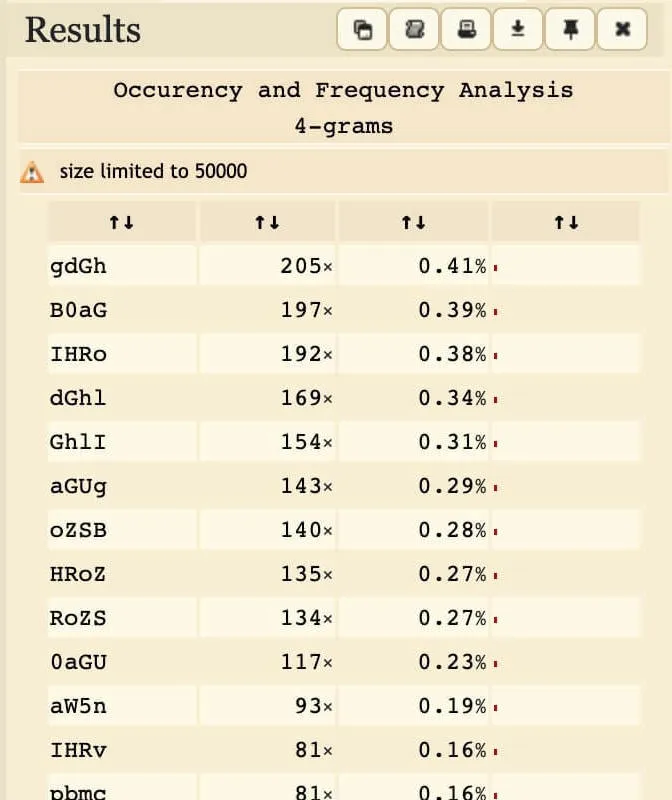
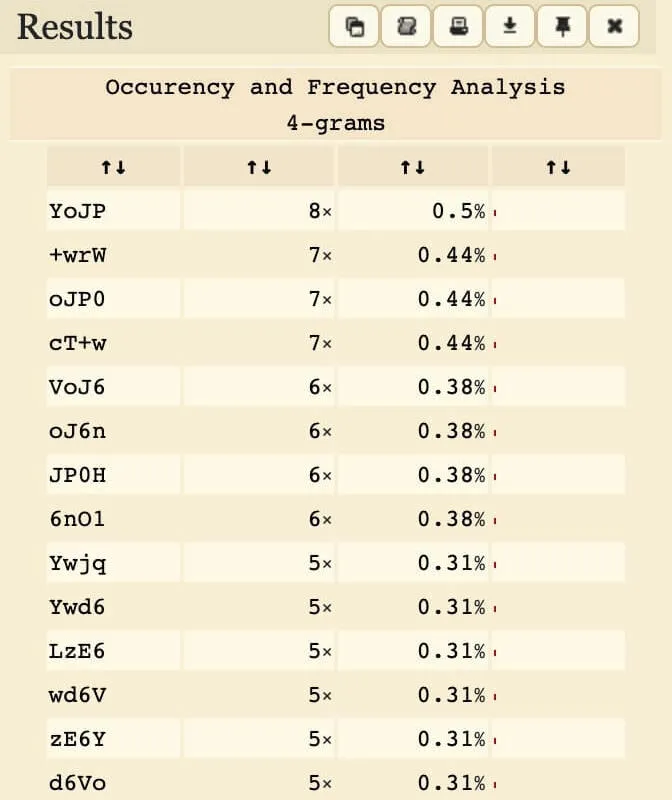
^{Frequency analysis of 4-grams in plain vs. encrypted Base64. Left: CNN Lite articles. Right: Encrypted challenge text.}

Observe how "YoJP0H" occurs (relatively) frequently. This corresponds to "IHRoZS", which happens to be the Base64 encoding for " the".

More Heuristics

Frequency analysis is useful to group letters into buckets. But using frequency analysis alone is painful. Some guesswork is needed. Here's the complete process I went through:

• Frequency Analysis: use dcode.fr to associate frequent characters.

  • We can make use of our earlier constraints to eliminate wrong guesses.³

    # Dictionary of guessed mappings.
    # key: shuffled Base64; value: plain Base64
    guesses = {
        'w': 'G',       'Y': 'I',
        'o': 'H',       'c': 'B',
    
        # " the "
        'J': 'R',       'P': 'o',
        '0': 'Z',       'H': 'S',
    
        # More snipped out.
        ...
    }
    for c, g in guesses.items():
        # Our guess should be whitelisted!
        assert set(g).issubset(whitelist[c]) for gc in g), f'mismatch for {c} -> {g}, whitelist: {whitelist[c]}'
        whitelist[c] = g # Throw away all other values.

    Python

    

    ^{Random decoding after frequency analysis.}

• Guesswork: guess English from the nonsense existing characters.

  • e.g. "Eog:ish" → "English", "qepqesents" → "represents", "pqese&ved" → "preserved"

  • Once we patched a word, other words became easier to patch.

    

    ^{Random decoding after guessing.}

  • At this point, we can continue patching "ciphertext", "letters", "potential", etc. Or we could just use...

• Google: after decoding a sizeable portion, let's pray and hope the plaintext is open-source. Then use the plaintext to derive the rest of the mapping.

  • It turns out the plaintext is—quite aptly—the Wikipedia summary of frequency analysis.

    

Finding the rest of the mappings was quite easy. After a bit more tuning, we get the flag.

Final Remarks

Usually I play reverse and don’t touch cryptography, but all I can say is: this was basically playing an English reverse challenge under the hood. Forget C, C++, Java, .Net, and Rust. Reversing English is the best. 😛

There are probably better ways to automatically perform frequency analysis and search for mappings. I went for a hybrid method of Python scripting + manually checking two dcode tabs. Perhaps a second monitor would’ve helped, but I have nowhere to place it. 😐

Flag

hkcert22{b4s3_s1x7y_f0ur_1s_4n_3nc0d1n9_n07_4n_encryp710n}