AOC 2021 Day 22 – Reactor Reboot

This post is a (very very late) writeup on solving the Advent of Code 2021 Day 22 challenge. This was one of the challenges I spent more time on, and ended up developing three algorithms (which is a bit overkill), all using set theory. I also ended up writing all three in both Haskell and Rust, and benchmarking to compare the runtimes. Needless to say, Rust ran about 25%-50% faster, but performance tuning is not the main point of this article.

I'll mainly show code snippets and implementations in Rust, well, because I think it's more readable. But the general ideas are similar in Haskell.

The Problem

It’s a fun, little problem. We're given a list of input. Each line specifies an action (on or off) and a cuboid (rectangular prism) of points x=10..12,y=10..12,z=10..12. Each line will switch all points within the cuboid on or off.

Sample input:

on x=10..12,y=10..12,z=10..12
on x=11..13,y=11..13,z=11..13
off x=9..11,y=9..11,z=9..11
on x=10..10,y=10..10,z=10..10

The objective is to determine the number of points that are still on after applying every line.

Solving

There are three main components to most of my AOC solves. For this challenge, we'll be implementing these functions.

1. fn parse(contents: String) -> Vec<Command> { ... },
2. fn part1(cmds: &Vec<Command>) -> u32 { ... }, and
3. fn part2(cmds: &Vec<Command>) -> u32 { ... }.

For Day 22, the only difference between part 1 and part 2 is the bound size, so a solution for part 2 would also be able to solve part 1 (but of course I didn't know this until later).

Parsing

Parsing is actually pretty straightforward, so let's get it out of the way first. Essentially, we translate each line of text to a 2-tuple: (bool, Cuboid).

// Some useful type aliases.
#[allow(non_camel_case_types)]
type cube_t = i64;

// Each pair corresponds to min/max values in a dimension.
type Cuboid = ((cube_t, cube_t), (cube_t, cube_t), (cube_t, cube_t));
struct Command(bool, Cuboid);

// Parse takes a String and returns a Vec of Commands.
fn parse(contents: String) -> Vec<Command> {
    let re = Regex::new(r"(on|off) x=(-?\d+)..(-?\d+),y=(-?\d+)..(-?\d+),z=(-?\d+)..(-?\d+)").unwrap();
    contents
        .lines() // Split text at lines.
        .map(|s| {
            for cap in re.captures_iter(s) { // Match with regex, and get capture groups.
                return Command(
                    // Capture group 0 is the entire matched string. So we start with 1, to obtain the first capture group.
                    cap[1].eq("on"),
                    (   // str's parse is builtin and returns an Option<_>.
                        (cap[2].parse::<cube_t>().unwrap(), cap[3].parse::<cube_t>().unwrap()),
                        (cap[4].parse::<cube_t>().unwrap(), cap[5].parse::<cube_t>().unwrap()),
                        (cap[6].parse::<cube_t>().unwrap(), cap[7].parse::<cube_t>().unwrap()),
                    ),
                );
            }
            unreachable!("aaaaaah") // Safety measure. We assume all lines follow the above pattern.
        })
        .collect()
}

A Naive Approach

Our first attempt may be to use a naive brute force approach. We keep track of every single point and whether it is toggled or not. Of course this will not scale well especially if the cubes become larger; but for part 1 of the challenge, it is sufficient. Part 1 simply confines the scope of our problem to ((-50, 50), (-50, 50), (-50, 50)). Any points activated or deactivated outside can be disregarded.

We can use a HashSet to store the 3D points. on would correspond with set.insert and off would correspond to set.remove. Thus after processing, we just need to count the number of elements (set.len()) to get the number of points that are left on.

Further, we’ll also restrict our scope by using .max and .min so that if, say x1 is way out there at -1000, x1.max(-r) will pull it back to -50.

// Solution 1: Brute-force Approach.
type Set = HashSet<(cube_t, cube_t, cube_t)>;

fn brute_force(cmds: &Vec<Command>) -> u32 {
    let mut set: Set = HashSet::new();
    let r = 50;
    for &Command(onoff, ((x1, x2), (y1, y2), (z1, z2))) in cmds {
        for i in x1.max(-r)..=x2.min(r) {
            for j in y1.max(-r)..=y2.min(r) {
                for k in z1.max(-r)..=z2.min(r) {
                    if onoff {
                        set.insert((i, j, k));
                    } else {
                        set.remove(&(i, j, k));
                    }
                }
            }
        }
    }
    set.len() as u32
}

Simple, right? Unfortunately for large cuboids this approach becomes extremely slow. By “large”, I mean cuboids like x=-100000..100000, y=-100000..100000, z=-100000..100000.

To deal with these big numbers, we need to bring in some big guns!

A Set Union Approach

In part 1, our scope was limited to a 100x100x100 cube centred on the origin. Part 2 removes this scope, meaning we have to take into account every single point in existence! Time to use this organ called the brain!

Let’s start with some investigative work and put on our thinking caps. For the moment, let’s imagine we’re working in 2D instead of 3D. Also, imagine our input is in some generic form.

^{$A$ on, $B$ on, $C$ on.}

^{$A$ on, $B$ off, $C$ on.}

When $A$ turns on, all the points in $A$ light up. Currently, we have $|A|$ points. Now let’s explore our next options.

• $B$ turns on. We now have $|A \cup B|$ points.
• $B$ turns off. How many points were switched off? Well, we simply subtract the intersection $|A \cap B|$, so that we end up with $|A| - |A \cap B| = |A \cup B| - |B|$ points.

Continuing further, we have

• $B$ on: $|A \cup B|$.

  • $C$ on → $|A \cup B \cup C|$ points.

  • $C$ off → Again, we subtract the intersection. $|A \cup B| - |(A \cup B) \cap C| = |A \cup B \cup C| - |C|$ points.

• $B$ off: $|A \cup B| - |B|$.

  • $C$ on → We want to add $|C|$, but suppose the points were already counted? We would need to subtract the double-counted points by considering the intersection of the new set $C$ and original points. We thus have—brace yourself—three new terms: $- |(A \cup B) \cap C|$, $+ |B \cap C|$, and $+ |C|$.

    $$ \underbrace{|A \cup B| - |B|}_{\text{original sets}} - \underbrace{|(A \cup B) \cap C| + |B \cap C|}_{\text{subtract double-counted}} + |C|. $$

    Regrouping and simplifying, we get

    $$ \begin{align*} &|A \cup B| + |C| - |(A \cup B) \cap C| - |B| + |B \cap C| \\ &= \underbrace{|A \cup B \cup C| - |B \cup C|}_{\text{original sets unioned with } C} + \underbrace{|C|}_{\text{new}}. \end{align*} $$

    Notice how we started off from $|A \cup B| - |B|$, and now we've simply extended them with $\cup\ C$ and added a $|C|$ term.

    This is actually similar to what we did when turning $B$ off the first time! We originally had $|A|$, then introduced $\cup\ B$, and subtracted $|B|$ so that we don’t count anything from $B$. We subtracted $|B|$ then, since we were turning $B$ off, but now we add $|C|$ since we’re turning $C$ on.

    Finally, let’s see what happens for the $A$ on, $B$ off, $C$ off case.

  • $C$ off → We can think of this as similar to the $B$ off $C$ on path above, except we don’t add the $|C|$ term. So we just have two terms:

    $$ \begin{align*} &\underbrace{|A \cup B \cup C| - |B \cup C| + |C|}_{\text{same as } B \text{ off, } C \text{ on}} - \underbrace{|C|}_{\text{new}} \\ &= |A \cup B \cup C| - |B \cup C|. \end{align*} $$

Notice that as we consider a new set, we union it with the previous sets. For example, $A$ on $B$ off has $|A \cup B| - |B|$ points. After adding $C$ off, we have $|A \cup B \cup C| - |B \cup C|$ points. Notice the similarity?

Moreover, we add a new term each time we change between on and off. We see this above in when going from $A$ on to $B$ off, from $B$ on to $C$ off, and $B$ off to $C$ on. Each time it’s one new term, and it’s the opposite sign of the previous term. It goes without saying, that this can be generalised.

Can we build it? Yes, we can!

Moving on to practical matters… how do we code this? We’ll separate the logic into two stages: one for building a set expression, the other for evaluating the expression.

Taking a lesson from functional programming, let’s discuss data and representation first. We can represent a union as a vector of cuboids: Vec<Cuboid>. But a cuboid is six integers, and the sets in our union all come from the input. So we can actually use a vector of indices instead: Vec<usize>. We’ll wrap these vectors in another container to represent our alternating union (this means every second term subtracts). I went for LinkedList for performance, but Vec should work as well.

Let’s build our set expression then:

let mut alternating_unions: LinkedList<Vec<usize>> = LinkedList::new();
let lookup = cmds.iter().map(|&Command(_, c)| c).collect::<Vec<_>>();
for (i, &Command(on, _)) in cmds.iter().enumerate() {
    for v in alternating_unions.iter_mut() {
        v.push(i); // Push the current tag.
    }
    if (alternating_unions.len() % 2 == 0) == on {
        // A new union term is added if "on" and even, or "off" and odd.
        let mut v = vec![i];
        v.reserve(cmds.len() - i); // Smol optimisation.
        alternating_unions.push_back(v);
    }
}

Evaluating the union is simply a matter of taking the set of unions, applying the inclusion-exclusion and generating a DFS tree with pruning. Those are some pretty big words. Let’s unpack it a bit.

What the heck is the Inclusion-Exclusion Principle?

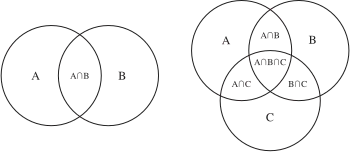
Given two sets $A$ and $B$, we can compute the union through $|A \cup B| = |A| + |B| - |A \cap B|$. The idea is that we add $A$ and $B$; but since we double-counted the overlapping region ($A \cap B$), we subtract it once to balance things out. It turns out this principle can be generalised for any number of sets.

Take a look at the diagram and convince yourself that for three sets, we have

$$ \begin{align*} |A\nobreak\cup\nobreak B\nobreak\cup\nobreak C| = &|A| + |B| + |C| \\ &- |A \cap B| - |A \cap C| - |B \cap C| \\ &+ |A \cap B \cap C|. \end{align*} $$

The inclusion-exclusion principle extends this idea to $n$ sets by including (adding) sets and excluding (subtracting) sets. The general formula for $n$ sets is

$$ \left| \bigcup_{i=0}^n A_i \right| = \sum_{k=1}^n (-1)^{k+1} \left( \sum_{1 \le i_1 < \cdots < i_k \le n} |A_{i_1} \cap \cdots \cap A_{i_k}| \right). $$

The Inclusion-Exclusion Principle as DFS

Earlier I mentioned DFS with pruning. Why DFS?

Let’s say we want to evaluate $|A \cup B \cup C|$. In a breadth-first approach, we would first evaluate the $k=1$ sets ($|A|$, $|B|$, $|C|$), followed by the $k=2$ sets ($|A \cap B|$, $|A \cap C|$, $|B \cap C|$), and so on. However, a depth-first approach would be more efficient in this case. Once we’ve computed $|A \cap B|$, we can compute $|A \cap B \cap C|$ as well.

Here’s a DFS tree for computing $|A \cup B \cup C|$:

A u B u C
|-- A
|   |-- A n B
|   |   |-- A n B n C
|   |
|   |-- A n C
|
|-- B
|   |-- B n C
|
|-- C

Can we parallelise this? Probably. But let’s leave that for another time.

Now what if two sets are disjoint? Suppose $A = ((0, 10), (0, 10), (0, 10))$ and $B = ((100, 200), (0, 10), (0, 10))$. These two sets have nothing in common, i.e. $A \cap B = \varnothing$. It follows that $A \cap B \cap C = \varnothing$. Thus, once we know a set has no intersection, we don’t need to further explore its branches. This is the pruning part of the DFS.

// @brief   Computes the number of points in a cuboid.
// @return  Number of points in a cuboid.
fn eval_cuboid(((x1, x2), (y1, y2), (z1, z2)): &Cuboid) -> u64 { ... }

// @brief   Computes the intersection of a cuboid.
// @return  Some(Cuboid) if the intersection exists, None otherwise.
fn intersect((x1, y1, z1): &Cuboid, (x2, y2, z2): &Cuboid) -> Option<Cuboid> { ... }

// @brief    Finds the intersection between two ranges.
// @return   Some((cube_t, cube_t)) if an intersection exists, None if there is no intersection.
fn range_intersect(&(a1, a2): &(cube_t, cube_t), &(b1, b2): &(cube_t, cube_t)) -> Option<(cube_t, cube_t)> { ... }

// @brief    eval_union computes the number of points in the union of sets `u`.
//
// @param    lookup: A lookup table of cuboids. Our sets will be represented as an array of indices (storing one i32 instead of six i32's).
// @param    add: Whether the current iteration adds or subtracts the union.
// @param    int: The current intersected cuboid.
// @param    u: The set of cuboids in the current union.
fn eval_union(lookup: &Vec<Cuboid>, add: bool, int: Cuboid, u: &[usize]) -> i64 {
    u.iter()
        .enumerate()
        .map(|(i, &tag)| match intersect(&int, &lookup[tag]) {
            Some(next_int) => {
                let v = eval_cuboid(&next_int) as i64;
                let rest = eval_union(lookup, !add, next_int, &u[i + 1..]);
                if add {
                    rest + v
                } else {
                    rest - v
                }
            }
            // No intersection. No need to evaluate deeper, since any intersection with the empty set will just be the empty set.
            None => 0,
        })
        .sum::<i64>()
}

let scope = ((-200000, 200000), (-200000, 200000), (-200000, 200000));
alternating_unions
    .iter()
    .enumerate()
    .map(|(i, u)| eval_union(&lookup, i % 2 == 0, scope, &u[..]))
    .sum::<i64>()

Final Remarks

This was one of the more challenging (but also rewarding!) Advent of Code challenges this year. Some others propose a cuboid-slicing method as opposed to set theory. However, I find this approach difficult to grasp and plan. Moreover, cuboid-slicing appears more difficult to generalise into higher dimensions, whereas with the set theoretic approach you pretty much just need to change the data types and intersect functions.

Anyway, let’s end on a pedagogical note. Here are some exercises for the reader:

• The set expression we built above contains some redundant information. What is redundant, and how can we optimise it?

• In the code above, we initialised our search with a scope.

  let scope = ((-200000, 200000), (-200000, 200000), (-200000, 200000));

  Rust

  Points outside the scope won’t be considered. Rewrite the evaluation logic so that a scope doesn’t need to be specified.

• In this post, we used a union-based approach, i.e. storing an alternating set of unions, then computing it by applying the inclusion-exclusion principle. Try rewriting the algorithm into an intersection-based approach. Instead of storing unions, store sets of intersections.

  • What are the computation differences?
  • Compare the two algorithms. Under what circumstances are one better?

Full Script

For completeness, here's the full d22.rs script.